
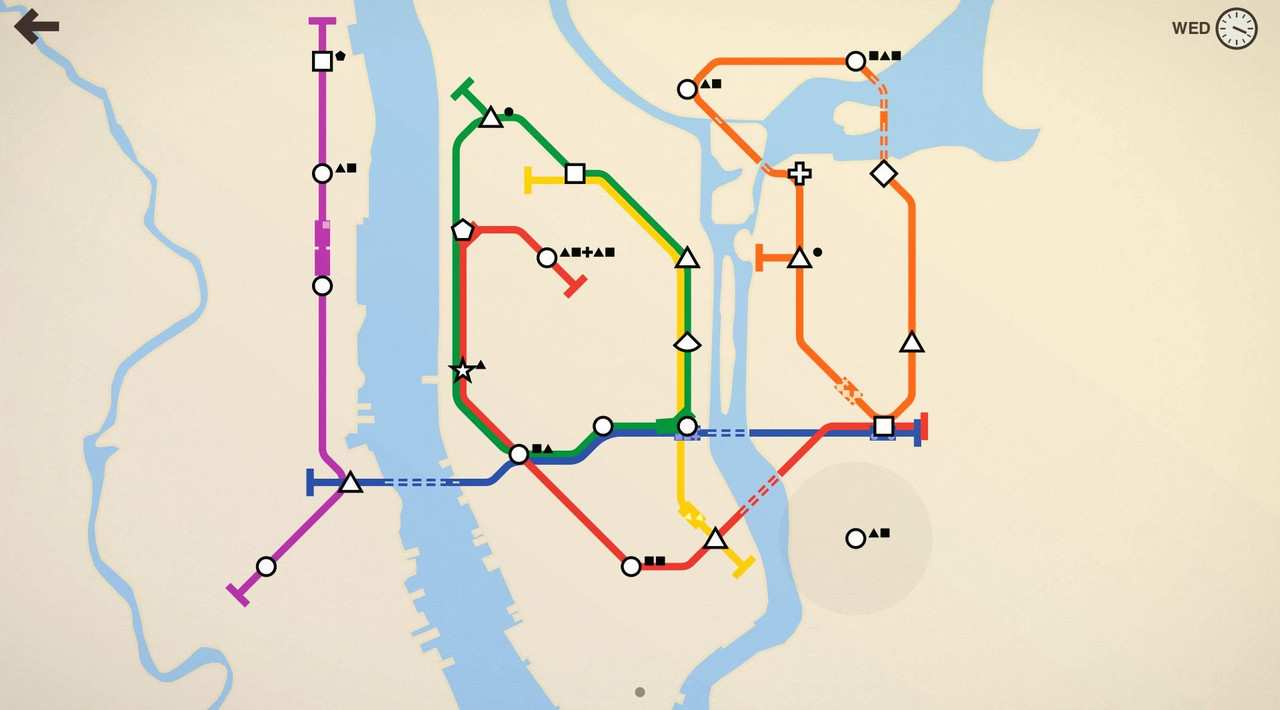
Now that you see the diagram just for that south portion, its time to look at the bigger map as a whole
MINI METRO COOL MATH UPGRADE
you do not need to know the specific odds or numbers or percentages but just keep in mind those odds and what weeks you need to pick up a carriage upgrade while at it.
MINI METRO COOL MATH PLUS
plus the multiple intersections allows you to not need a carriage as specific lines just needs to pick up their passengers and just move along. it is because the amount of loops and lines dealing with that area have trains that are constantly moving from station to station without having to wait for an another train to come by and pick up. Now im going to focus on the south of the seine river where itll be easier for me to add lines and stations and to calculate the odds and likelihood for needing a carriage upgrade just for the south of the seine.Īs you can see, as more lines started to add onto the area, your chances of needing a carriage goes smaller and you do not need to worry about getting a carriage on that side of the river. If you still dont understand the math behind this, let me use the beautiful vintage paris 1937 metro map as a demonstration this also means that in about 3 weeks, you must get at least one carriage upgrade for those lines. since you have 3 lines going into or on that area, the probability of you needing a carriage to place on those lines are 1 in 3 chances or 33.333%. Take for an example, say that i have a loop and 2 lines crossing over a river on the eastern edge of the map. the likelihood of you needing to get a carriage also depends on the amount of weeks you are considering in getting a carriage upgrade for that area. because of how many trains go through that area, you do not need as much carriages for that area since the trains spontaneously go in and out delivering those sets of passengers. The inverse equation for deciding how much carriages goes on a particular set of linesĪs you can see from what i listed, this is an inverse function where as your lines on an area increases, the odds of you needing to place a carriage on that same area exponentially decreases. keep in mind that i am not a mathematician wizard and just a junior in high school and only had a grasp on just algebra, calculus and a little bit of statistics.


well after thinking about it, i came up with a equation that reflects off of that statement. That thought came in my mind when i had multiple lines over in guangzhou that didnt need much carriages as from the southern portion of the map. The amount of lines in a particular area is inversely proportional to the amount of carriages needed for that same area On a comment thread that i listed on my last mini metro post, i left a bolded statement where that but seeing how much i observed just from playing it makes me wonder what kind of possibility i can take to get on that path of making sure i can get where i needed to score high. it seems that the strategy that i always take is quickly getting as much lines before moving along to carriages and i found some success while achieving it. WARNING: if you despise algebra and statistics or cannot bear to watch some simple equations or numbers, may i advice you to move along and continue on without thinking about thisįor the few of you remaining, i found a concept while playing guangzhou just recently on my other post and the other maps that got me to close or near the leaderboards whether its daily or all-time.


 0 kommentar(er)
0 kommentar(er)
